S:E20.56: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| Line 6: | Line 6: | ||
'''Soluție''' | '''Soluție''' | ||
Cum ''<math>\sphericalangle A = 36^\circ</math>'' și triunghiul ''<math>ABC</math>'' este isoscel, se obține că <math>\sphericalangle B = \sphericalangle C = 72^\circ</math>. Atunci <math>\sphericalangle ABD = \sphericalangle DBC = 36^\circ</math>, deci \sphericalangle | Cum ''<math>\sphericalangle A = 36^\circ</math>'' și triunghiul ''<math>ABC</math>'' este isoscel, se obține că <math>\sphericalangle B = \sphericalangle C = 72^\circ</math>. Atunci <math>\sphericalangle ABD = \sphericalangle DBC = 36^\circ</math>, deci <math>\sphericalangle BDC = 72^\circ</math>. | ||
Cum <math>DE</math> este mediatoarea segmentului <math>AD</math>, rezultă că <math>AED</math> este un triunghi isoscel, cu <math>\sphericalangle A = \sphericalangle D = 36^\circ</math>, deci <math>\sphericalangle AED = 108^\circ</math>. Atunci <math>\sphericalangle BED = 72^\circ</math>, ceea ce implică <math>\sphericalangle EDB = 72^\circ</math>. | |||
În concluzie, <math>\sphericalangle BDC = \sphericalangle EDB= 72^\circ</math>, ceea ce impică faptul că <math>DB</math> este bisectoare pentru unghiul <math>CDE</math>. | |||
Revision as of 08:08, 7 January 2025
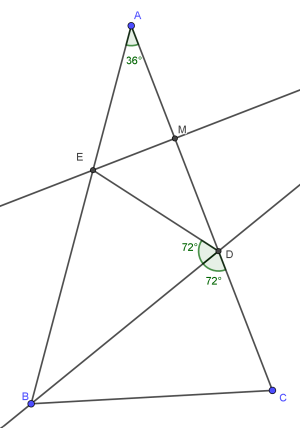
S:E20.56 (Cristina Vijdeluc, Mihai Vijdeluc)
Se consideră triunghiul , cu și . Punctul aparține laturii astfel încât este bisectoarea unghiului . Mediatorarea segmentului intersectează latura în . Arătați că este bisectoare pentru unghiul .
Soluție
Cum și triunghiul este isoscel, se obține că . Atunci , deci .
Cum este mediatoarea segmentului , rezultă că este un triunghi isoscel, cu , deci . Atunci , ceea ce implică .
În concluzie, , ceea ce impică faptul că este bisectoare pentru unghiul .




















