14527: Difference between revisions
No edit summary |
No edit summary |
||
| Line 11: | Line 11: | ||
Începem cu partea stângă a egalității <math>\left( n+1\right) \cdot \left(n+1\right) ! - n \cdot n !</math> | Începem cu partea stângă a egalității <math>\left( n+1\right) \cdot \left(n+1\right) ! - n \cdot n !</math> | ||
Avem <math> (n+ 1) ! = (n + 1) \cdot n! </math>, deci | Avem <math> (n+ 1) ! = (n + 1) \cdot n! </math>, deci <math> (n + 1) \cdot (n + 1) ! = (n + 1)^2 · n!</math>. Atunci, membrul din partea stângă a egalității devine <math>(n + 1)^2 \cdot n! − n \cdot n!</math>. | ||
(n + 1) | |||
(n + 1)2 | |||
Factorizăm n!: | Factorizăm n!: | ||
Revision as of 12:26, 2 January 2025
E:14527 (Cristina Vijdeluc şi Mihai Vijdeluc)
Pentru orice număr natural nenul Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} , notăm Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n! = 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n} și Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0! = 1} .
a) Arătați că Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( n+1\right) \cdot \bigl(n+1\bigr) ! - n \cdot n ! = \left( n^2 + n + 1 \right) \cdot n ! }
b) Dacă Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \left( 60^2 + 60 + 1\right) \cdot 60 ! + \left( 59^2 + 59 + 1\right) \cdot 59! + \ldots + \left( 1^2 + 1 + 1\right) \cdot 1! + (0^2 + 0 + 1) \cdot 0!} , atunci Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} se divide cu Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2013^2} .
Soluție
Începem cu partea stângă a egalității Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( n+1\right) \cdot \left(n+1\right) ! - n \cdot n !}
Avem Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (n+ 1) ! = (n + 1) \cdot n! } , deci Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (n + 1) \cdot (n + 1) ! = (n + 1)^2 · n!} . Atunci, membrul din partea stângă a egalității devine Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (n + 1)^2 \cdot n! − n \cdot n!} .
Factorizăm n!:
= n!((n + 1)² − n)
Calculăm (n + 1)² − n:
(n + 1)² − n = n² + 2n + 1 − n = n² + n + 1
Astfel, partea stângă devine:
n! · (n² + n + 1)
Deci, am demonstrat că:
(n + 1) · (n + 1)! − n · n! = (n² + n + 1) · n!
b) Dacă A = (60² + 60 + 1) · 60! + (59² + 59 + 1) · 59! +. . . + (1² + 1 + 1) · 1! + (0² + 0 + 1) · 0!, atunci A se
divide cu 2013².
Soluție
Observăm că fiecare termen din sumă poate fi scris astfel:
k² + k + 1 = (k + 1)² − k
Astfel, putem rescrie A:
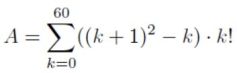
Separăm suma:
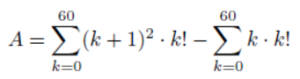
Calculăm fiecare sumă în parte. Prima sumă devine:
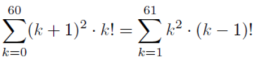
Folosind identitatea k2 · (k − 1)! = k! · k + k!:
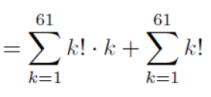
A doua sumă este:
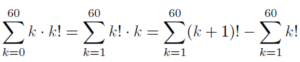
Astfel, putem scrie:
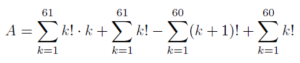
Observăm că termenii se simplifică, iar suma finală devine:
A = 61! + 60! + 1
Acum, să verificăm dacă A se divide cu 2013². Observăm că:
Astfel, putem scrie:
2013 = 3 · 11 · 61
2013² = (3 · 11 · 61)² = ²2 · 11² · 61²
Acum, să verificăm dacă A = 61! + 60! + 1 se divide cu 2013².
- **Divizibilitatea cu 32**: - Atât 61! cât și 60! cont, in factori de 3, deci 61! + 60! este divizibil cu 3. - De asemenea, 1 nu este divizibil cu 3, dar suma 61! + 60! este mult mai mare decât 1 și va conține suficienți factori de 3 pentru a asigura divizibilitatea cu 3².
- **Divizibilitatea cu 11²**: - Similar, atât 61! cât și 60! conțin factori de 11, deci 61! + 60! este divizibil cu 11. - Din nou, 1 nu afectează divizibilitatea generală, iar suma va conține suficienți factori de 11 pentru a asigura divizibilitatea cu 11².
- **Divizibilitatea cu 61²**: - Atât 61! cât și 60! conțin factori de 61, deci 61! + 60! este divizibil cu 61. - La fel ca și în cazurile anterioare, 1 nu afectează divizibilitatea generală, iar suma va conține suficienți factori de 61 pentru a asigura divizibilitatea cu 61².
Prin urmare, am demonstrat că A se divide cu 2013².