(One intermediate revision by the same user not shown) Line 1:
Line 1: '''[[28868]] (Andre Horvat-Marc)'''
'''[[28868]] (Andrei Horvat-Marc)'''
''Fie <math>n\in \mathbb{N^\ast}</math> și funcțiile <math>f:\left[0,2n^2+3n\right] \to \left[1,2n+1\right]</math>, <math> f\left(x\right) = \frac{\sqrt{8x+9}-1}{2}</math> ''și ''<math> g:\left[1,2n+1\right] \to \left[0,2n^2+3n\right]</math>, <math> g\left(x\right) = f^{-1}\left(x\right)</math>.''
''Fie <math>n\in \mathbb{N^\ast}</math> și funcțiile <math>f:\left[0,2n^2+3n\right] \to \left[1,2n+1\right]</math>, <math> f\left(x\right) = \frac{\sqrt{8x+9}-1}{2}</math> ''și ''<math> g:\left[1,2n+1\right] \to \left[0,2n^2+3n\right]</math>, <math> g\left(x\right) = f^{-1}\left(x\right)</math>.''
Line 26:
Line 26: Se obține
Se obține
<math display="block">M_n = \dfrac{1}{6}\left(12n^4+28n^3-3n^2-43n+24\right), n\in \mathbb{N}^\ast.</math>
<math display="block">M_n = \dfrac{1}{6}\left(12n^4+28n^3-3n^2-43n+24\right), n\in \mathbb{N}^\ast.</math>
[[File:Laticeale-5-2024.png|thumb|304x304px]]
'''Cazuri particulare:'''
'''Cazuri particulare:'''
<math>M_1 = 3</math> este ușor de construit și verificat,
<math>M_1 = 3</math> este ușor de construit și verificat,
[[File:Laticeale-5-2024.png|thumb|304x304px]]
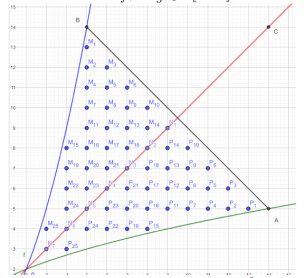
<math>M_2 = 57</math> este reprezentat în figura alăturată,
<math>M_2 = 57</math> este reprezentat în figura alăturată,
28868 (Andrei Horvat-Marc)
Fie
n
∈
N
∗
{\displaystyle n\in \mathbb {N^{\ast }} }
f
:
[
0
,
2
n
2
+
3
n
]
→
[
1
,
2
n
+
1
]
{\displaystyle f:\left[0,2n^{2}+3n\right]\to \left[1,2n+1\right]}
f
(
x
)
=
8
x
+
9
−
1
2
{\displaystyle f\left(x\right)={\frac {{\sqrt {8x+9}}-1}{2}}}
și
g
:
[
1
,
2
n
+
1
]
→
[
0
,
2
n
2
+
3
n
]
{\displaystyle g:\left[1,2n+1\right]\to \left[0,2n^{2}+3n\right]}
g
(
x
)
=
f
−
1
(
x
)
{\displaystyle g\left(x\right)=f^{-1}\left(x\right)}
Fie punctele
A
(
2
n
2
+
3
n
,
2
n
+
1
)
{\displaystyle A\left(2n^{2}+3n,2n+1\right)}
B
(
2
n
+
1
,
2
n
2
+
3
n
)
{\displaystyle B\left(2n+1,2n^{2}+3n\right)}
și mulțimea
M
{\displaystyle M}
f
{\displaystyle f}
g
{\displaystyle g}
A
B
{\displaystyle AB}
M
{\displaystyle M}
Soluție.
Cum
g
=
f
−
1
{\displaystyle g=f^{-1}}
g
:
[
1
,
2
n
+
1
]
→
[
0
,
2
n
2
+
3
n
]
{\displaystyle g:\left[1,2n+1\right]\to \left[0,2n^{2}+3n\right]}
g
(
x
)
=
(
x
−
1
)
(
x
+
2
)
2
{\displaystyle g\left(x\right)={\dfrac {\left(x-1\right)\left(x+2\right)}{2}}}
g
(
k
)
∈
N
{\displaystyle g\left(k\right)\in \mathbb {N} }
k
∈
[
1
,
2
n
+
1
]
∩
N
{\displaystyle k\in \left[1,2n+1\right]\cap \mathbb {N} }
Avem
B
(
2
n
+
1
,
2
n
2
+
3
n
)
∈
G
g
{\displaystyle B\left(2n+1,2n^{2}+3n\right)\in G_{g}}
A
(
2
n
2
+
3
n
,
2
n
+
1
)
∈
G
f
{\displaystyle A\left(2n^{2}+3n,2n+1\right)\in G_{f}}
G
f
∩
G
g
=
{
D
(
2
,
2
)
}
{\displaystyle G_{f}\cap G_{g}=\left\{D\left(2,2\right)\right\}}
Au loc inegalitățile
f
(
x
)
≤
x
{\displaystyle f\left(x\right)\leq x}
x
∈
[
2
,
2
n
2
+
3
n
]
{\displaystyle x\in \left[2,2n^{2}+3n\right]}
g
(
x
)
≥
x
{\displaystyle g\left(x\right)\geq x}
x
∈
[
2
,
2
n
+
1
]
{\displaystyle x\in \left[2,2n+1\right]}
Considerăm că mulțimea
M
{\displaystyle M}
A
B
D
{\displaystyle ABD}
A
B
D
{\displaystyle ABD}
M
n
{\displaystyle M_{n}}
Între segmentele
G
f
{\displaystyle G_{f}}
G
g
{\displaystyle G_{g}}
Q
(
1
,
1
)
{\displaystyle Q\left(1,1\right)}
M
{\displaystyle M}
G
f
{\displaystyle G_{f}}
G
g
{\displaystyle G_{g}}
[
A
B
]
{\displaystyle \left[AB\right]}
Fie punctele
C
(
2
n
2
+
3
n
,
2
n
2
+
3
n
)
{\displaystyle C\left(2n^{2}+3n,2n^{2}+3n\right)}
E
(
2
,
2
n
2
+
3
n
)
{\displaystyle E\left(2,2n^{2}+3n\right)}
F
(
2
n
2
+
3
n
,
2
)
{\displaystyle F\left(2n^{2}+3n,2\right)}
D
B
E
{\displaystyle DBE}
D
A
F
{\displaystyle DAF}
Notăm cu
A
n
{\displaystyle A_{n}}
D
F
C
E
{\displaystyle DFCE}
T
n
{\displaystyle T_{n}}
C
A
B
{\displaystyle CAB}
S
n
{\displaystyle S_{n}}
D
B
E
{\displaystyle DBE}
Avem
A
n
=
(
2
n
2
+
3
n
−
1
)
2
,
{\displaystyle A_{n}=\left(2n^{2}+3n-1\right)^{2},}
T
n
=
∑
k
=
1
2
n
2
+
n
k
=
1
2
n
(
2
n
+
1
)
(
2
n
2
+
n
+
1
)
,
{\displaystyle T_{n}=\sum \limits _{k=1}^{2n^{2}+n}k={\dfrac {1}{2}}n\left(2n+1\right)\left(2n^{2}+n+1\right),}
și
S
n
=
∑
k
=
2
2
n
+
1
(
2
n
2
+
3
n
+
1
−
g
(
k
)
)
=
1
3
n
(
2
n
+
1
)
(
4
n
+
1
)
.
{\displaystyle S_{n}=\sum \limits _{k=2}^{2n+1}\left(2n^{2}+3n+1-g\left(k\right)\right)={\dfrac {1}{3}}n\left(2n+1\right)\left(4n+1\right).}
Atunci
M
n
=
A
n
−
2
S
n
−
T
n
+
3
,
{\displaystyle M_{n}=A_{n}-2S_{n}-T_{n}+3,}
în formula precedenă de adaugă
3
{\displaystyle 3}
pentru a corecta faptul că punctele
A
{\displaystyle A}
,
B
{\displaystyle B}
, respectiv
D
{\displaystyle D}
, sunt puncte comune ale regiunilor
A
D
F
{\displaystyle ADF}
,
B
D
E
{\displaystyle BDE}
, respectiv
C
A
B
{\displaystyle CAB}
.
Se obține
M
n
=
1
6
(
12
n
4
+
28
n
3
−
3
n
2
−
43
n
+
24
)
,
n
∈
N
∗
.
{\displaystyle M_{n}={\dfrac {1}{6}}\left(12n^{4}+28n^{3}-3n^{2}-43n+24\right),n\in \mathbb {N} ^{\ast }.}
Cazuri particulare:
M
1
=
3
{\displaystyle M_{1}=3}
M
2
=
57
{\displaystyle M_{2}=57}
M
3
=
266
{\displaystyle M_{3}=266}
M
4
=
778
{\displaystyle M_{4}=778}
Observație
Problema de mai sus este echivalentă cu următoarea problemă
Fie
n
∈
N
∗
{\displaystyle n\in \mathbb {N} ^{\ast }}
f
:
[
0
,
2
n
2
+
3
n
]
→
[
1
,
2
n
+
1
]
{\displaystyle f:\left[0,2n^{2}+3n\right]\to \left[1,2n+1\right]}
f
(
x
)
=
8
x
+
9
−
1
2
{\displaystyle f\left(x\right)={\dfrac {{\sqrt {8x+9}}-1}{2}}}
S
(
n
)
=
∑
k
=
0
2
n
2
+
3
n
[
f
(
k
)
]
{\displaystyle S\left(n\right)=\sum \limits _{k=0}^{2n^{2}+3n}\left[f\left(k\right)\right]}
[
a
]
{\displaystyle \left[a\right]}
a
∈
R
{\displaystyle a\in \mathbb {R} }

![{\displaystyle f:\left[0,2n^{2}+3n\right]\to \left[1,2n+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/223f445094a9520da8ece8c78b5f1e7b39cdb113)

![{\displaystyle g:\left[1,2n+1\right]\to \left[0,2n^{2}+3n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbdd17f8999a9a0914ddf96ce2f0ad88a7a77a18)










![{\displaystyle k\in \left[1,2n+1\right]\cap \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd6758cde9d2f90a8cc7e80ee4486a3a45c18a4c)




![{\displaystyle x\in \left[2,2n^{2}+3n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63094ff03dda2b712355ebc95c0ea93152989898)

![{\displaystyle x\in \left[2,2n+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5ea232e56c14826656246d0b51606e9e1911951)





![{\displaystyle \left[AB\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5040ef57543bf16f0c5fe301ba25f4a5a457836b)



























![{\displaystyle S\left(n\right)=\sum \limits _{k=0}^{2n^{2}+3n}\left[f\left(k\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bae5d0d711cf7a5e610289a6cafa502b71e93a7c)
![{\displaystyle \left[a\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76984b1ba4f30272a4b22c033dd18093f9566686)
