28868: Difference between revisions
No edit summary |
mNo edit summary |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
'''[[28868]] ( | '''[[28868]] (Andrei Horvat-Marc)''' | ||
''Fie <math>n\in \mathbb{N^\ast}</math> și funcțiile <math>f:\left[0,2n^2+3n\right] \to \left[1,2n+1\right]</math>, <math> f\left(x\right) = \frac{\sqrt{8x+9}-1}{2}</math> ''și ''<math> g:\left[1,2n+1\right] \to \left[0,2n^2+3n\right]</math>, <math> g\left(x\right) = f^{-1}\left(x\right)</math>.'' | ''Fie <math>n\in \mathbb{N^\ast}</math> și funcțiile <math>f:\left[0,2n^2+3n\right] \to \left[1,2n+1\right]</math>, <math> f\left(x\right) = \frac{\sqrt{8x+9}-1}{2}</math> ''și ''<math> g:\left[1,2n+1\right] \to \left[0,2n^2+3n\right]</math>, <math> g\left(x\right) = f^{-1}\left(x\right)</math>.'' | ||
| Line 5: | Line 5: | ||
''Fie punctele'' <math>A\left(2n^2+3n,2n+1\right)</math>, <math>B\left(2n+1,2n^2+3n\right)</math> ''și mulțimea <math>M</math> a punctelor din plan cuprinse între graficele funcțiilor <math>f</math> și <math>g</math> și dreapta <math>AB</math>. Aflați numărul punctelor din <math>M</math> care au ambele coordonate întregi.'' | ''Fie punctele'' <math>A\left(2n^2+3n,2n+1\right)</math>, <math>B\left(2n+1,2n^2+3n\right)</math> ''și mulțimea <math>M</math> a punctelor din plan cuprinse între graficele funcțiilor <math>f</math> și <math>g</math> și dreapta <math>AB</math>. Aflați numărul punctelor din <math>M</math> care au ambele coordonate întregi.'' | ||
'''Soluție''' | '''Soluție.''' | ||
Cum <math>g = f^{-1}</math>, se obține că funcția <math>g:\left[1,2n+1\right] \to \left[0,2n^2+3n\right]</math> este definită prin <math>g\left(x\right) = \dfrac{\left(x-1\right)\left(x+2\right)}{2}</math>. Mai mult, <math>g\left(k\right) \in \mathbb{N}</math> oricare ar fi <math>k \in \left[1, 2n+1\right] \cap \mathbb {N}</math>. | |||
Avem <math>B\left(2n+1,2n^2+3n\right) \in G_g</math>, <math>A\left(2n^2+3n,2n+1\right) \in G_f </math> și <math>G_f \cap G_g = \left\{D\left(2,2\right)\right\}</math>. | |||
Au loc inegalitățile <math>f\left(x\right) \le x</math> oricare ar fi <math>x \in \left[2,2n^2+3n\right]</math> și <math>g\left(x\right) \ge x</math> oricare ar fi <math>x \in \left[2, 2n+1\right]</math>. | |||
Considerăm că mulțimea <math>M</math> este mulțimea tuturor punctelor din plan cuprinse în interiorul triunghiului curbiliniu <math>ABD</math>, deci este necesar să numărăm punctele laticeale din interiorul triunghiului curbiliniu <math>ABD</math>, vom nota cu <math>M_n</math> acest număr. | |||
Între segmentele <math>G_f</math> și <math>G_g</math> se situează și punctul <math>Q\left(1,1\right)</math>, însă considerăm <math>M</math> ca fiind mulțimea închisă delimitată de <math>G_f</math>, <math>G_g</math> și <math>\left[AB\right]</math>. | Între segmentele <math>G_f</math> și <math>G_g</math> se situează și punctul <math>Q\left(1,1\right)</math>, însă considerăm <math>M</math> ca fiind mulțimea închisă delimitată de <math>G_f</math>, <math>G_g</math> și <math>\left[AB\right]</math>. | ||
Fie punctele <math>C\left(2n^2+3n,2n^2+3n\right)</math>, <math>E\left(2,2n^2+3n\right)</math>, <math>F\left(2n^2+3n,2\right)</math> și | Fie punctele <math>C\left(2n^2+3n,2n^2+3n\right)</math>, <math>E\left(2,2n^2+3n\right)</math>, <math>F\left(2n^2+3n,2\right)</math>. Observăm că, datorită simetriei, triunghiurile curbilinii <math>DBE</math> și <math>DAF</math> conțin același număr de puncte laticeale. | ||
<math> | |||
Notăm cu <math>A_n</math> numărul punctelor laticeale din interiorul și de pe frontiera pătratului <math>DFCE</math>., cu <math>T_n</math> numărul punctelor laticeale din interiorul și de pe frontiera triunghiului <math>CAB</math> și cu <math> | |||
S_n</math> numărul punctelor laticeale din interiorul și de pe frontiera triunghiului curbiliniu <math>DBE</math>. | |||
Avem <math>A_n = \left(2n^2+3n-1\right)^2</math> | Avem <math display="block">A_n = \left(2n^2+3n-1\right)^2,</math> <math display="block">T_n = \sum\limits_{k=1}^{2n^2+n} k = \dfrac{1}{2}n\left(2n+1\right)\left(2n^2+n+1\right), </math> și <math display="block">S_n = \sum\limits_{k=2}^{2n+1} \left(2n^2+3n+1-g\left(k\right)\right) = \dfrac{1}{3}n\left(2n+1\right)\left(4n+1\right).</math>Atunci <math display="block">M_n = A_n - 2S_n -T_n+3,</math>în formula precedenă de adaugă <math>3</math> pentru a corecta faptul că punctele <math>A</math>, <math>B</math>, respectiv <math>D</math>, sunt puncte comune ale regiunilor <math>ADF</math>, <math>BDE</math>, respectiv <math>CAB</math>. | ||
Atunci <math>M_n = A_n - 2S_n -T_n+3</math> | |||
<math>M_n = \dfrac{1}{6}\left(12n^4+28n^3-3n^2-43n+24\right), | Se obține | ||
Cazuri particulare: <math>M_1 = 3</math> este ușor de construit și verificat, <math>M_2 = 57</math> este reprezentat în figura | <math display="block">M_n = \dfrac{1}{6}\left(12n^4+28n^3-3n^2-43n+24\right), n\in \mathbb{N}^\ast.</math> | ||
[[File:Laticeale-5-2024.png|thumb|304x304px]] | |||
'''Cazuri particulare:''' | |||
<math>M_1 = 3</math> este ușor de construit și verificat, | |||
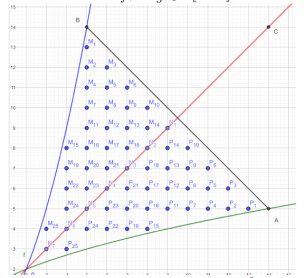
<math>M_2 = 57</math> este reprezentat în figura alăturată, | |||
<math>M_3 = 266 </math> și <math>M_4 = 778</math>. | |||
'''Observație''' | |||
Problema de mai sus este echivalentă cu următoarea problemă | |||
''Fie <math>n\in \mathbb{N}^\ast</math> un număr natural și funcția <math>f:\left[0,2n^2+3n\right]\to \left[1,2n+1\right]</math>, cu <math>f\left(x\right) = \dfrac{\sqrt{8x+9}-1}{2}</math>. Determinați valoarea sumei <math> S\left(n\right)=\sum\limits_{k=0}^{2n^2+3n} \left[f\left(k\right)\right]</math>, unde prin <math>\left[a\right]</math> s-a notat partea întreagă a numărului real <math>a\in \mathbb{R}</math>.'' | |||
Latest revision as of 08:27, 4 August 2025
28868 (Andrei Horvat-Marc)
Fie și funcțiile , și , .
Fie punctele , și mulțimea a punctelor din plan cuprinse între graficele funcțiilor și și dreapta . Aflați numărul punctelor din care au ambele coordonate întregi.
Soluție.
Cum , se obține că funcția este definită prin . Mai mult, oricare ar fi .
Avem , și .
Au loc inegalitățile oricare ar fi și oricare ar fi .
Considerăm că mulțimea este mulțimea tuturor punctelor din plan cuprinse în interiorul triunghiului curbiliniu , deci este necesar să numărăm punctele laticeale din interiorul triunghiului curbiliniu , vom nota cu acest număr.
Între segmentele și se situează și punctul , însă considerăm ca fiind mulțimea închisă delimitată de , și .
Fie punctele , , . Observăm că, datorită simetriei, triunghiurile curbilinii și conțin același număr de puncte laticeale.
Notăm cu numărul punctelor laticeale din interiorul și de pe frontiera pătratului ., cu numărul punctelor laticeale din interiorul și de pe frontiera triunghiului și cu numărul punctelor laticeale din interiorul și de pe frontiera triunghiului curbiliniu .
Avem
Se obține
Cazuri particulare:
este ușor de construit și verificat,
este reprezentat în figura alăturată,
și .
Observație Problema de mai sus este echivalentă cu următoarea problemă
Fie un număr natural și funcția , cu . Determinați valoarea sumei , unde prin s-a notat partea întreagă a numărului real .

![{\displaystyle f:\left[0,2n^{2}+3n\right]\to \left[1,2n+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/223f445094a9520da8ece8c78b5f1e7b39cdb113)

![{\displaystyle g:\left[1,2n+1\right]\to \left[0,2n^{2}+3n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbdd17f8999a9a0914ddf96ce2f0ad88a7a77a18)










![{\displaystyle k\in \left[1,2n+1\right]\cap \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd6758cde9d2f90a8cc7e80ee4486a3a45c18a4c)




![{\displaystyle x\in \left[2,2n^{2}+3n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63094ff03dda2b712355ebc95c0ea93152989898)

![{\displaystyle x\in \left[2,2n+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5ea232e56c14826656246d0b51606e9e1911951)





![{\displaystyle \left[AB\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5040ef57543bf16f0c5fe301ba25f4a5a457836b)



























![{\displaystyle S\left(n\right)=\sum \limits _{k=0}^{2n^{2}+3n}\left[f\left(k\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bae5d0d711cf7a5e610289a6cafa502b71e93a7c)
![{\displaystyle \left[a\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76984b1ba4f30272a4b22c033dd18093f9566686)
