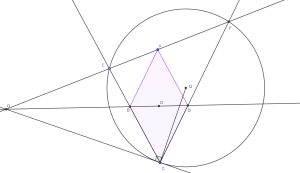
E:5756 (Dumitru Acu)
Fie
A
B
C
D
{\displaystyle ABCD}
A
{\displaystyle A}
B
C
{\displaystyle BC}
E
{\displaystyle E}
D
C
{\displaystyle DC}
F
{\displaystyle F}
B
D
{\displaystyle BD}
G
{\displaystyle G}
C
G
{\displaystyle CG}
C
{\displaystyle C}
E
C
F
{\displaystyle ECF}
Soluție
Din faptul că semidreapta
(
D
B
{\displaystyle (DB}
∢
A
D
C
{\displaystyle \sphericalangle ADC}
(
G
B
{\displaystyle (GB}
∢
A
G
C
{\displaystyle \sphericalangle AGC}
[
A
G
]
≡
[
C
G
]
{\displaystyle \left[AG\right]\equiv \left[CG\right]}
În triunghiul
F
G
C
{\displaystyle FGC}
Teorema bisectoarei , pentru bisectoarea
(
G
D
{\displaystyle (GD}
∢
F
G
C
{\displaystyle \sphericalangle FGC}
C
D
D
F
=
G
C
G
F
{\displaystyle {\frac {CD}{DF}}={\frac {GC}{GF}}}
Cum patulaterul
A
B
C
D
{\displaystyle ABCD}
este un romb, avem
A
B
∥
B
C
{\displaystyle AB\parallel BC}
, deci
Teorema lui Thales implică
C
D
D
F
=
E
A
A
F
{\displaystyle {\frac {CD}{DF}}={\frac {EA}{AF}}}
Atunci avem
E
A
A
F
=
G
A
G
F
⇒
E
A
G
A
=
A
F
G
F
{\displaystyle {\frac {EA}{AF}}={\frac {GA}{GF}}\Rightarrow {\frac {EA}{GA}}={\frac {AF}{GF}}}
Prin intermediul proporțiilor derivate se obține
G
A
−
A
E
G
A
=
G
F
−
F
A
G
F
⇒
G
E
G
A
=
G
A
G
F
,
{\displaystyle {\frac {GA-AE}{GA}}={\frac {GF-FA}{GF}}\Rightarrow {\frac {GE}{GA}}={\frac {GA}{GF}},}
ceea ce revine la
G
A
2
=
G
E
⋅
G
F
⇔
G
C
2
=
G
E
⋅
G
F
.
{\displaystyle GA^{2}=GE\cdot GF\Leftrightarrow GC^{2}=GE\cdot GF.}
Din puterea punctului
G
{\displaystyle G}
E
{\displaystyle E}
C
{\displaystyle C}
F
{\displaystyle F}
G
C
{\displaystyle GC}
E
C
F
{\displaystyle ECF}















![{\displaystyle \left[AG\right]\equiv \left[CG\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bc9687c30dcc014ccc21012c4a0caceb469a5b7)









