15685: Difference between revisions
Insert image |
mNo edit summary |
||
| Line 4: | Line 4: | ||
'''Soluție''' | '''Soluție''' | ||
Deoarece <math> AM </math> este mediana în triunghiul dreptunghic <math> ABC </math> avem <math> AM = BM = CM </math>. Din <math> AM = BM </math> rezultă că <math> \triangle AMB\ </math> este isoscel și, cum <math>ME \perp AB</math>, <math>ME</math> este bisectoarea unghiului <math> AMB </math>. Cum <math> \angle B\ = 30^\circ </math> și <math> ME \perp AB </math> obținem <math> \angle EMB\ = 60^\circ </math>, de unde <math> \angle AME\ = 60^\circ, (1) </math>. Pe de altă parte <math> \angle AMC\ </math> este unghi exterior triunghiului <math> AMB </math> și atunci <math> \angle AMC\ = 60^\circ, (2) </math>. Din <math> (1) </math> și <math> (2) </math> deducem că <math> MA </math> este bisectoarea unghiului <math> DME, (3) </math>. | |||
Deoarece <math> AM </math> este mediana în triunghiul dreptunghic <math> ABC </math> avem <math> AM = BM = CM </math>. Din <math> AM = BM </math> rezultă că <math> \triangle AMB\ </math> este isoscel și, cum <math>ME \perp AB</math>, <math>ME</math> este bisectoarea unghiului <math> AMB </math>. Cum <math> \angle B\ = 30^\circ </math> și <math> ME \perp AB </math> obținem <math> \angle EMB\ = 60^\circ </math>, de unde <math> \angle AME\ = 60^\circ, (1) </math>. | |||
Pe de altă parte <math> \angle AMC\ </math> este unghi exterior triunghiului <math> AMB </math> și atunci <math> \angle AMC\ = 60^\circ, (2) </math>. | |||
Din <math> (1) </math> și <math> (2) </math> deducem că <math> MA </math> este bisectoarea unghiului <math> DME, (3) </math>. | |||
[[File:Gm e-15685.png|left|thumb]] | [[File:Gm e-15685.png|left|thumb]] | ||
Din <math> AM = CM </math> și <math> \angle AMC\ = 60^\circ </math> rezultă că <math> \triangle AMC\ </math> este echilateral și, cum <math> AD \perp BC </math>, deducem că <math> D </math> este mijlocul segmentului <math> CM </math>, deci <math> DM = CM | |||
Din <math> AM = CM </math> și <math> \angle AMC\ = 60^\circ </math> rezultă că <math> \triangle AMC\ </math> este echilateral și, cum <math> AD \perp BC </math>, deducem că <math> D </math> este mijlocul segmentului <math> CM </math>, deci <math> DM = \frac{1}{2}\cdot CM, (4) </math>. | |||
Din <math> \triangle BEM\ </math> este dreptunghic și <math> \angle B\ = 30^\circ </math> obținem <math> ME = \frac{1}{2}\cdot BM, (5) </math>. | |||
Cum <math> CM = BM </math>, din <math> (4) </math> și <math> (5) </math> rezultă <math> DM = EM </math>, adică <math> \triangle DME\ </math> este isoscel. De aici și din <math> (3) </math> rezultă <math> MA \perp DE </math>. | |||
Latest revision as of 05:05, 12 December 2024
E:15685 (Cristina Vijdeliuc și Mihai Vijdeliuc)
Se consideră triunghiul dreptunghic , cu și . Punctul aparține laturii astfel încât , punctul este mijlocul segmentului , iar punctul aparține laturii astfel încât . Arătați că .
Soluție
Deoarece este mediana în triunghiul dreptunghic avem . Din rezultă că este isoscel și, cum , este bisectoarea unghiului . Cum și obținem , de unde .
Pe de altă parte este unghi exterior triunghiului și atunci .
Din și deducem că este bisectoarea unghiului .
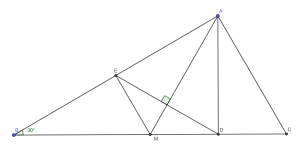
Din și rezultă că este echilateral și, cum , deducem că este mijlocul segmentului , deci .
Din este dreptunghic și obținem .
Cum , din și rezultă , adică este isoscel. De aici și din rezultă .






































