E:16899: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
'''[[E:16899]] (Angela Lopată)''' | '''[[E:16899]] (Angela Lopată)''' | ||
''Fie <math>ABC</math> un triunghi pentru care lungimea proiecţiei laturii <math>AB</math> pe dreapta <math>BC</math> este mai mare decât lungimea segmentului <math>\left[AC\right]</math>. | ''Fie <math>ABC</math> un triunghi pentru care lungimea proiecţiei laturii <math>AB</math> pe dreapta <math>BC</math> este mai mare decât lungimea segmentului <math>\left[AC\right]</math>. Considerăm punctele <math>M</math>, <math>N</math> pe laturile <math>\left(BC\right)</math>, respectiv <math>\left(AC\right)</math> astfel încât <math>BM = CN</math>. Fie punctul <math>P</math> astfel încât <math>NM = MP</math>, punctele <math>N</math> și <math>P</math> sunt de aceeași parte a dreptei <math>BC</math>, iar distanţa de la punctul <math>P</math> la dreapta <math>BC</math> este aceeași cu distanţa de la punctul <math>M</math> la dreapta <math>AC</math>. Arătaţi că <math>\sphericalangle NMP = \sphericalangle PBM = \sphericalangle MCA</math>.'' | ||
'''Soluție''' | '''Soluție.''' | ||
[[File:16898.png|center|thumb]] | [[File:16898.png|center|thumb]] | ||
| Line 15: | Line 15: | ||
\end{cases}</math>, conform cazului de congruenţă L.U.L., rezultă <math>\Delta PMB \equiv \Delta MNC</math>, deci <math>\sphericalangle PBC = \sphericalangle MCN</math>. | \end{cases}</math>, conform cazului de congruenţă L.U.L., rezultă <math>\Delta PMB \equiv \Delta MNC</math>, deci <math>\sphericalangle PBC = \sphericalangle MCN</math>. | ||
Cum punctele <math>B</math>, <math>M</math> și <math>C</math> sunt colinare, avem | Cum punctele <math>B</math>, <math>M</math> și <math>C</math> sunt colinare, avem <math display="block" id="e16899-1" qid="e16899-1">\sphericalangle BMP + \sphericalangle PMN + \sphericalangle NMC = 180^\circ. | ||
<math>\sphericalangle BMP + \sphericalangle PMN + \sphericalangle NMC = 180^\circ. | </math> | ||
</math> | |||
În triunghiul <math>\Delta CMN</math> avem <math display="block" id="e16899-2" qid="e16899-2">\sphericalangle CNM + \sphericalangle NMC + \sphericalangle MCN = 180^\circ. | |||
</math> | |||
Din cele două egalități și <math>\sphericalangle PMB = \sphericalangle MNC</math> se deduce <math>\sphericalangle PMN = \sphericalangle MCN</math>. | |||
În concluzie, are loc egalitatea <math display="block">\sphericalangle NMP = \sphericalangle PBM = \sphericalangle MCA.</math> | |||
Latest revision as of 16:20, 19 August 2025
E:16899 (Angela Lopată)
Fie un triunghi pentru care lungimea proiecţiei laturii pe dreapta este mai mare decât lungimea segmentului . Considerăm punctele , pe laturile , respectiv astfel încât . Fie punctul astfel încât , punctele și sunt de aceeași parte a dreptei , iar distanţa de la punctul la dreapta este aceeași cu distanţa de la punctul la dreapta . Arătaţi că .
Soluție.
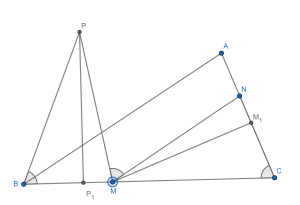
Din , conform cazului de congruenţă C.I., rezultă , deci .
Din , conform cazului de congruenţă L.U.L., rezultă , deci .
Cum punctele , și sunt colinare, avem
În triunghiul avem
Din cele două egalități și se deduce .
În concluzie, are loc egalitatea



![{\displaystyle \left[AC\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75221e2f8dfb66a48aec1498c809c414321762ff)





















